gaussplotR provides functions to fit two-dimensional Gaussian functions, predict values from such functions, and produce plots of predicted data.
Installation
You can install gaussplotR from CRAN via:
install.packages("gaussplotR")Or to get the latest (developmental) version through GitHub, use:
devtools::install_github("vbaliga/gaussplotR")Example
The function fit_gaussian_2D() is the workhorse of gaussplotR. It uses stats::nls() to find the best-fitting parameters of a 2D-Gaussian fit to supplied data based on one of three formula choices. The function autofit_gaussian_2D() can be used to automatically figure out the best formula choice and arrive at the best-fitting parameters.
The predict_gaussian_2D() function can then be used to predict values from the Gaussian over a supplied grid of X- and Y-values (generated here via expand.grid()). This is useful if the original data is relatively sparse and interpolation of values is desired.
Plotting can then be achieved via ggplot_gaussian_2D(), but note that the data.frame created by predict_gaussian_2D() can be supplied to other plotting frameworks such as lattice::levelplot(). A 3D plot can also be produced via rgl_gaussian_2D() (not shown here).
library(gaussplotR)
## Load the sample data set
data(gaussplot_sample_data)
## The raw data we'd like to use are in columns 1:3
samp_dat <-
gaussplot_sample_data[,1:3]
#### Example 1: Unconstrained elliptical ####
## This fits an unconstrained elliptical by default
gauss_fit_ue <-
fit_gaussian_2D(samp_dat)
## Generate a grid of X- and Y- values on which to predict
grid <-
expand.grid(X_values = seq(from = -5, to = 0, by = 0.1),
Y_values = seq(from = -1, to = 4, by = 0.1))
## Predict the values using predict_gaussian_2D
gauss_data_ue <-
predict_gaussian_2D(
fit_object = gauss_fit_ue,
X_values = grid$X_values,
Y_values = grid$Y_values,
)
## Plot via ggplot2 and metR
library(ggplot2); library(metR)
#> Warning: package 'ggplot2' was built under R version 4.0.5
#> Warning: package 'metR' was built under R version 4.0.5
ggplot_gaussian_2D(gauss_data_ue)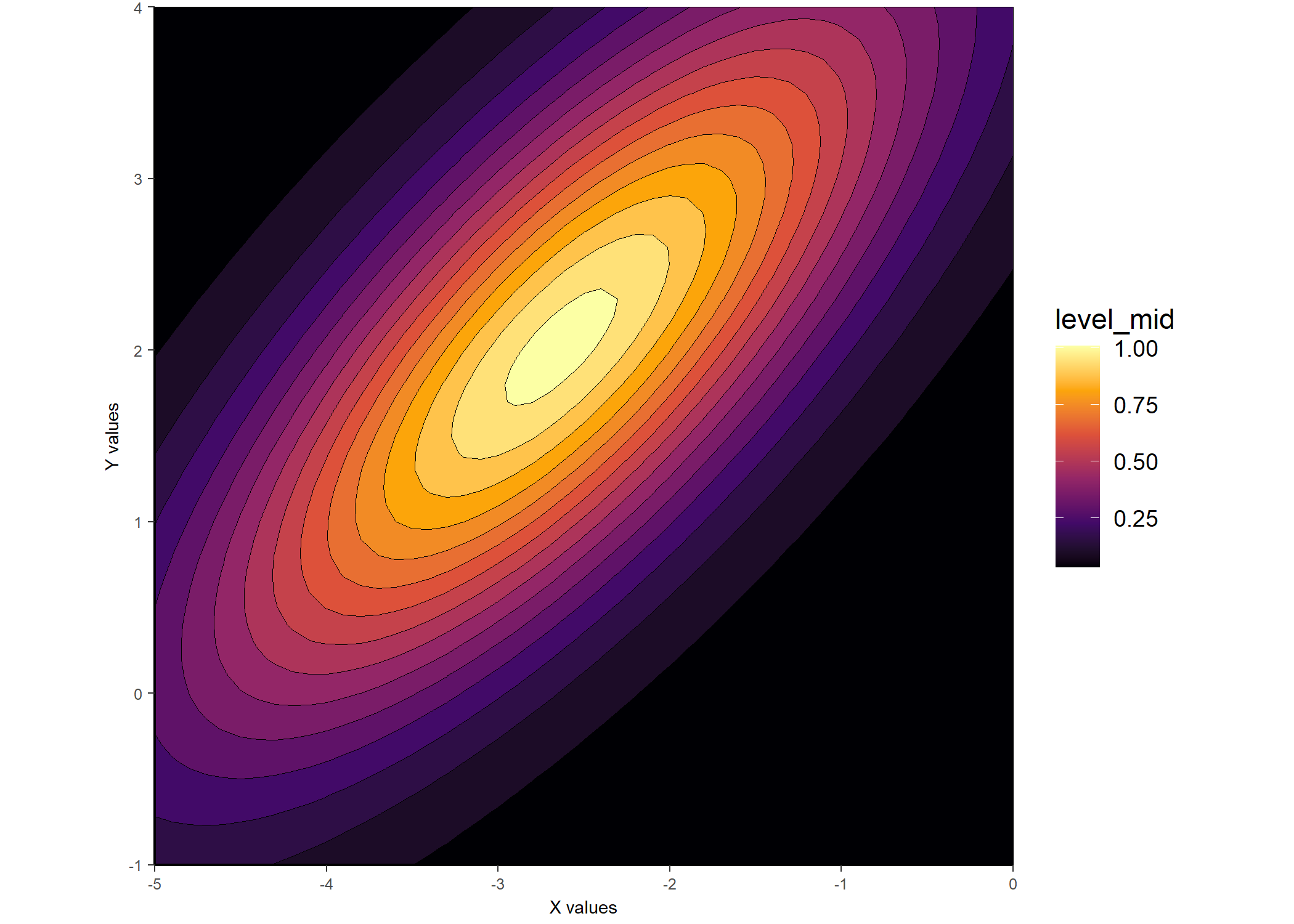
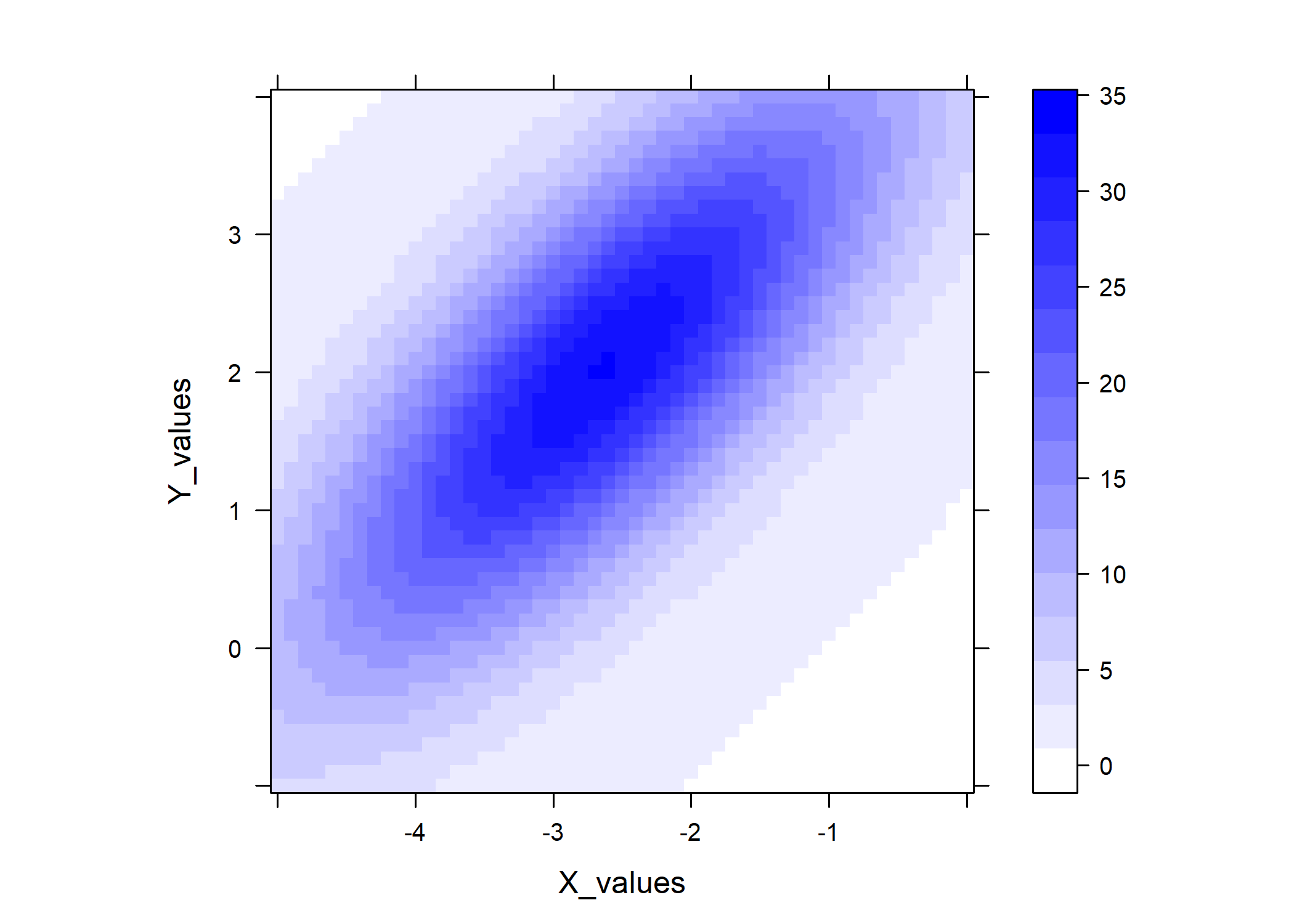
## And another example plot via lattice::levelplot()
library(lattice)
lattice::levelplot(
predicted_values ~ X_values * Y_values,
data = gauss_data_ue,
col.regions = colorRampPalette(
c("white", "blue")
)(100),
asp = 1
)
#### Example 2: Constrained elliptical_log ####
## This fits a constrained elliptical, as in Priebe et al. 2003
gauss_fit_cel <-
fit_gaussian_2D(
samp_dat,
method = "elliptical_log",
constrain_orientation = -1
)
## Generate a grid of x- and y- values on which to predict
grid <-
expand.grid(X_values = seq(from = -5, to = 0, by = 0.1),
Y_values = seq(from = -1, to = 4, by = 0.1))
## Predict the values using predict_gaussian_2D
gauss_data_cel <-
predict_gaussian_2D(
fit_object = gauss_fit_cel,
X_values = grid$X_values,
Y_values = grid$Y_values,
)
## Plot via ggplot2 and metR
ggplot_gaussian_2D(gauss_data_cel)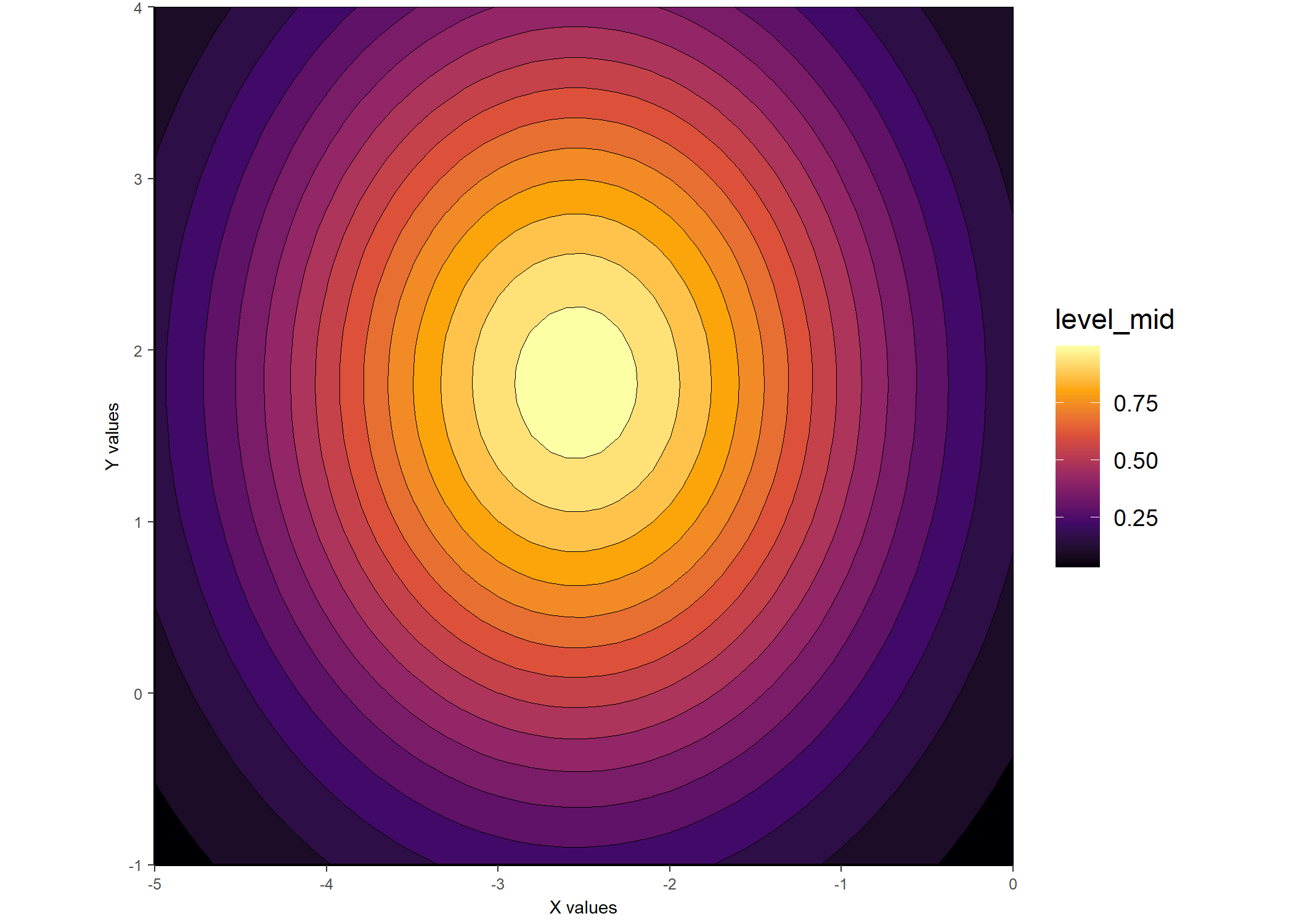
Should you be interested in having gaussplotR try to automatically determine the best choice of method for fit_gaussian_2D(), the autofit_gaussian_2D() function can come in handy. The default is to select the method that produces a fit with the lowest rmse, but other choices include rss and AIC.
## Use autofit_gaussian_2D() to automatically decide the best
## model to use
gauss_auto <-
autofit_gaussian_2D(
samp_dat,
comparison_method = "rmse",
simplify = TRUE
)
## The output has the same components as `fit_gaussian_2D()`
## but for the automatically-selected best-fitting method only:
summary(gauss_auto)
#> Model coefficients
#> A_o Amp theta X_peak Y_peak a b
#> 0.83 32.25 3.58 -2.64 2.02 0.91 0.96
#> Model error stats
#> rss rmse deviance AIC
#> 156.23 2.08 156.23 171
#> Fitting methods
#> method amplitude orientation
#> "elliptical" "unconstrained" "unconstrained"Contributing and/or raising Issues
Feedback on bugs, improvements, and/or feature requests are all welcome. Please see the Issues templates on GitHub to make a bug fix request or feature request.
To contribute code via a pull request, please consult the Contributing Guide first.
Citation
Baliga, VB. 2021. gaussplotR: Fit, predict, and plot 2D-Gaussians in R. Journal of Open Source Software, 6(60), 3074. https://doi.org/10.21105/joss.03074
